During a recent red team engagement, we came across several useful artefacts after compromising an IT helpdesk user account. One of particular interest contained a list of useful sites, including a well-known password generator site. This is one of a class of sites that generate a password by selecting a number, say 4, random words and joining them together.
But why call the article Three Random Words and not Four? Well, the UK government cybersecurity arm, the NCSC, recommend users to use three random words [1]. To quote:
“Weak passwords can be cracked in seconds. The longer and more unusual your password is, the harder it is for a cyber criminal to crack.
A good way to make your password difficult to crack is by combining three random words to create a password (for example applenemobiro). Or you could use a password manager, which can create strong passwords for you (and remember them).“
Later in the engagement we managed to exfiltrate the Active Directory database (ntds.dit) by downloading one of their domain controllers.
This brings us to the core of this article – cracking the NTLM hashes. After performing the standard attacks, we managed to crack about 30% of the user accounts but struggled to get beyond that. Naturally we decided to look at passwords generated via these types of sites.
Password Generator Sites
In this article we will look at two password generator sites:
- https://correcthorsebatterystaple.com/ which we will refer to as CHBS
- https://correcthorse.pw/ which we will refer to as CHPW
Both these have a simple interface to configure the types of password to generate; typically joining a defined number of words together with an optional separator, potential capitalization, and the use of a digit.
The words themselves are a short dictionary. CHPW include the list (8192 words) in the code so that it is all generated in the browser, whilst CHBS doesn’t; but we do have a link to a github site containing a dictionary of 4980 words [2]. Combining and removing duplicates this adds up to 9459 words.
Whilst a short list, the number of combinations will rapidly increase. Assuming we use 9473 words, without the numbers or symbols then:
- 2 words = 9473 * 9473 = 89,737,729 combinations
- 3 words = 9473 * 9473 * 9473 = 850,085,506,817 combinations
- 4 words = 8,052,860,006,077,441 combinations
In a real attack we would also add a few target-specific words, like the company name, key products, locations or subsidiaries.
The Attack
Given the size of the dataset, how can we attack this?
First, people like the easiest route. Why have four random words when three will do? Providing the password meets the technically enforced corporate policy, why change the defaults? This represents a good starting point for our approach.
The typical CHPW password would be something like debtor-sad-vulture-material, but corporate policies usually require uppercase, lowercase, a symbol and a digit. So, lets capitalize the words and add a digit. However, as we feel four words are a lot, lets reduce that to three. This gives us something like Cherry-Precedence-Head-7.
As for CHBS we might have something like bell-fixture-inch6. Interestingly, this site doesn’t append any digit, but only a “6”.
The approach we will take is known as a Combinator Attack [3]. Here we can take two smaller dictionaries and generate candidate words that combine each word in the first dictionary with each word in the second. The key here is it saves storage space.
A second benefit with the Combinator Attack in hashcat is that is allows us to include a single rule to apply to each dictionary.
Stage 0 – The Hardware
In this blog I will be using my laptop for the hash cracking. This has a decent but not high-end GPU – a Nvidia RTX A2000. Here a benchmark rate for NTLM hashes is:
Speed.#1………: 22017.2 MH/s (59.65ms) @ Accel:128 Loops:1024 Thr:512 Vec:1
Compare this to an RTX 4090:
Speed.#1………: 288.5 GH/s (7.24ms) @ Accel:512 Loops:1024 Thr:32 Vec:8
In other words, the cracking rate is going to be significantly faster on dedicated cracking hardware that would typically have these higher-end GPU’s – and several of them. Whilst some of the later attacks will be challenging on the laptop, they will not be on a dedicated rig.
Stage 1 – Preparing the attack
First things we need are wordlists. For reasons that will become apparent later, I’m creating three wordlists:
- A list of all words with the first letter capitalised – e.g. Abbot
- A list of all combinations of two words, separated by space, with each word capitalised, just as for the list of single words – e.g. Abbot Head
- A list of all words with the first letter capitalised followed by a space then a single digit (one for each digit 0-9) – e.g. Abbot 3
As expected from our calculations, the hybrid lists are quite small:

This result will allow us to try all standard combinations that use one, two, three or four words.
Stage 2 – The first attack
In our discussion we mentioned one form of password that looks like Cherry-Precedence-Head-7. How can we guarantee that we will find that password?
What we are going to do is combine the two-word dictionary (ch-all-double.txt) with the single+digit dictionary (ch-all-single-digit.txt). However, our dictionaries separate the words with spaces and not dashes.
Fortunately, during a combinator attack, hashcat has two extremely useful flags. First, “-j” which applies a single rule to the first/left dictionary. Second, “-k” applies a single rule to the second/right dictionary.
The following table represents key rules for us. Indeed, the capitalised wordlists and these rules are sufficient to generate all key “standard” combinations.
| Rule | Description |
| C | Capitalise the first letter and lowercase the rest. |
| l | Lowercase all letters |
| sAB | Replace all occurrences of the character A with the character B |
| $A | Append the character A to the end of the string |
| @A | Purge all instances of the character A |
See [4] for a reference to more hashcat rules.
In our first wordlist we will have listed the word “Cherry Precedence” and in the second “Head 7”. By using the rule “s -$-“ to the first wordlist and the rule “s -“ to the second wordlist we will transform them to “Cherry-Precedence-“ and “Head-7”. When hashcat comes across these words and performs the rule transform the result will be the password Cherry-Precedence-Head-7.
If we just wanted the first word capitalised, then the left side is “cs -$-“ and right side “ls -“.
One other note, several of these passwords are going to be longer than 27 characters. If it is likely users will use them, we cannot use the hashcat “-O” optimised kernel but the pure kernel. This will dramatically slow down the attempt. In this case you either need to accept it or go with optimised first for quick wins and re-run with the pure kernel for full coverage.
The command for finding passwords like Cherry-Precedence-Head-7 will be something like:
hashcat -m 1000 -d 1 -a 1 ..\toCrack\demo-ntlm.txt ..\wordlists\m0noc\ch-all-double.txt ..\wordlists\m0noc\ch-all-single-digit.txt -j “s -$-“ -k “s -“
So, what does this look like on a laptop with a standard GPU?
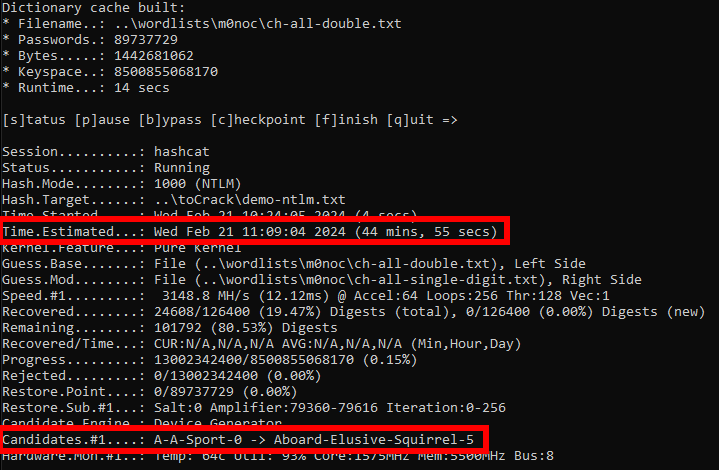
45 minutes to test all three-word CHPW password using the options of capitalise words and append a digit. As this is the pure kernel, we are not constrained to 27 characters. Dedicated hardware will be significantly faster.
If we choose to use the optimized kernel the estimated time on our laptop is more than halved:

If we are looking for all two-word forms of this, we have two choices:
- Use the single word and the “single word+digit” list
- Use the double word list as a normal attack and open up full rulesets like best66.rule – you can still use the “-j” flag.
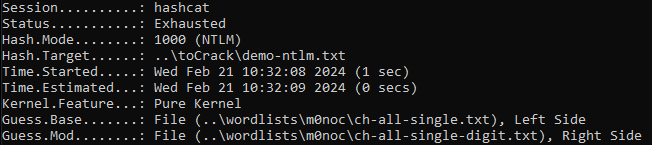
The two single word lists are trivial (approx. 1 second for a billion guesses):
We can use the full ruleset like this:
hashcat -m 1000 -d 1 ..\toCrack\demo-ntlm.txt ..\wordlists\m0noc\ch-all-double.txt ..\wordlists\m0noc\ch-all-single-digit.txt -j “s -“ -r ..\rules\git-20240122\best66.rule
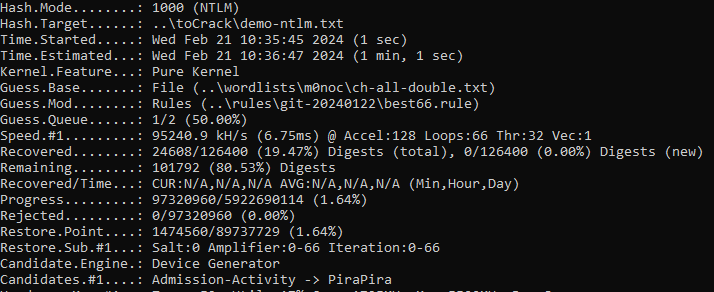
As you can see; with only two words trying large complex variations is trivial.
Stage 3 – Doing the rounds
The CHBS passwords include those like bell-fixture-inch6. In this case the digit is always 6. If we’re using the standard options, we can test all combinations in under 6 minutes.
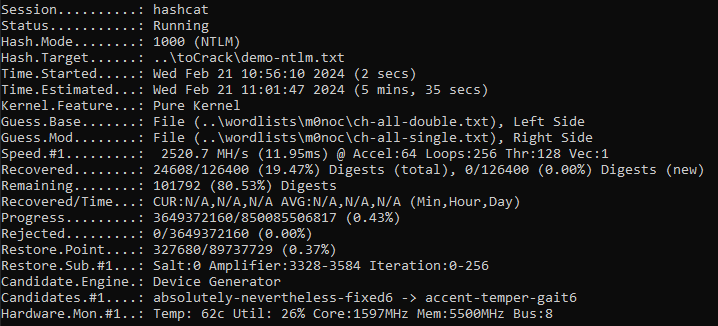
If we want to test for all single digit passphrases, we can do something like the following, which reverts us back to the 45 minute estimates under the pure kernel.
hashcat -m 1000 -d 1 -a 1 ..\toCrack\demo-ntlm.txt ..\wordlists\m0noc\ch-all-double.txt ..\wordlists\m0noc\ch-all-single-digit.txt -j “ls -$-“ -k “l@ ”

Of course, manually typing this is annoying. Given the options for the keyspace, I naturally wrote a script to generate a batch file with all the variations in options. I could then run that to ensure all three-word combinations had been tried.

This represents 192 hashcat commands at circa 6 minutes each – 20 hours for the pure kernel or 10 hours for the optimised kernel.
Why do we have a problem?
Three random words suffers from the likely choice of words. If people use password generator sites, the list of words is often of insufficient length (our combined list of words in this example is circa 10,000) – you can even play with what-three-words style lists as well! Effectively there is low entropy.
If people recommend “random words” style passwords, as a minimum we would recommend four random words from a much larger set of words.
The second issue is a more technical one. We still have passwords stored using weak unsalted hashing algorithms in key infrastructure like Active Directory. If the contents of that database get compromised, then we can generate massive lists of passwords to try.
For example, where NTLM hashes on my laptop have a maximum cracking rate of circa 22017.2 MH/s, bcrypt is significantly harder:

Even newer hashing algorithms like Argon2 are designed to be GPU resistant.
References
[1] https://www.ncsc.gov.uk/collection/top-tips-for-staying-secure-online/three-random-words
[2] https://github.com/paulanthonywilson/correct-horse-elixir
[3] https://hashcat.net/wiki/doku.php?id=combinator_attack
[4] https://hashcat.net/wiki/doku.php?id=rule_based_attack